Different approaches for finding Motifs in DNA sequences with Python

Rosalind is a great way to create and experiment with different algorithms from the computational world and apply them to biological questions. There are different possibilities on how to find substrings (or motifs) within a string (DNA sequence). Here, I would like to try out four different approaches, one-by-one and test them with the dataset provided by Rosalind. Rosalind - Finding a Motif in DNA

Author

Affiliation

Franziska Ahrend

Published

Jul. 13, 2022

DOI

The problem “subs - Finding a Motif in DNA” has the assignment to find all matches of a motif in a given string. The sample dataset is as followed:

Sample input

GATATATGCATATACTT 
ATAT

Sample output

2 4 10

In theory, I have learned different algorithms on how to solve such problems. Now I want to apply them to this (and eventually bigger) datasets.

I will discuss four different algorithms to find motifs in a DNA sequence:

Naive Approach - Pattern Matching Problem

KMP: Knuth-Morris-Pratt

Rabin-Carp

Bozer-Moore

Load data

Even though these strings are really fast copied and pasted into my IDE, I like to always consider how this would be possible (especially with Rosalind’s time limit of 5 minutes) when the data is much larger in size or quantity. Then command+C and command+V is not the best option; it just takes too much time and RAM.

f = open('rosalind_subs.txt', 'r')
subsList = f.read().split()
s = subsList[0]
t = subsList[1]

So I used the functions open(), read() and then split() to get the strings from the downloaded dataset. In this case you do not need to split the txt file in any complicated way, but just by line separation. This splits the text in multiple (here just 2) strings and stores them in a list. The DNA and the Motif can be received by their indices.

Here, what is finally stored in both variables s and t:

print('DNA (s):', s)
print('\nMotif to find (t):',t)

DNA (s): CCAGTGGGGTTAGTGCAGTGGGCAGTGGGCAGTGGGGGACGCTGAGCGTCAGTGGGCAGTGGGGGCCATAATGAAACGTGTCACATGCAAATACAGTGGGGGAGCAGTGGGCAGTGGGCCAGTGGGCAGTGGGTGGGACCAGTGGGCAGTGGGGTATTCAGTGGGGCAGTGGGCAGTGGGCAGTGGGAATTCAAATTCAGTGGGCAGTGGGCAGTGGGCTGCCTTCCCAGTGGGCAGTGGGATGCCAGTGGGCCCAGTGGGTAGGCAGTGGGTCAGTGGGGACTCAGTGGGCGCAGTGGGACCAGTGGGCAGTGGGCACAGTGGGAAGGCAGTGGGAAGCAGTGGGCACAGTGGGCTTTCCAGTGGGTCAGTGGGCGGTCACAGTGGGCAGTGGGCAGTGGGTCAGTGGGGGGCAGTGGGGCAGTGGGTACAGTGGGGAACCAGTGGGTTCCTATCCACGTCAGTGGGCAGTGGGACAGTGGGGGCCAGTGGGCAGTGGGCAGTGGGCAGTGGGTATTTCCAGTGGGCAGTGGGCAGTGGGTCAGTGGGATCAGGCAGTGGGTATCCCCTATGCAGCAGCGGCAGCAGTGGGCAATTCTCAGTGGGTAGCGGGCGCGGTGCAGTGGGCAGTGGGTGCAGTGGGGTGCAGTGGGATCAGTGGGCTCACGTCAGTGGGCCCAGTGGGCATAGGTGTGTACAGTGGGACAGTGGGCAGTGGGCAGACAGTGGGACAGTGGGCAGTGGGGCAGTGGGCAGTGGGTCGCAGTGGGTGCAGTGGGCTGGCAGTGGGCAGTGGGCCAGTGGGACTTCAGTGGG 

Motif to find (t): CAGTGGGCA

You can prepare this before actually getting the first (large) dataset and before you can simply practice with the small sample dataset.

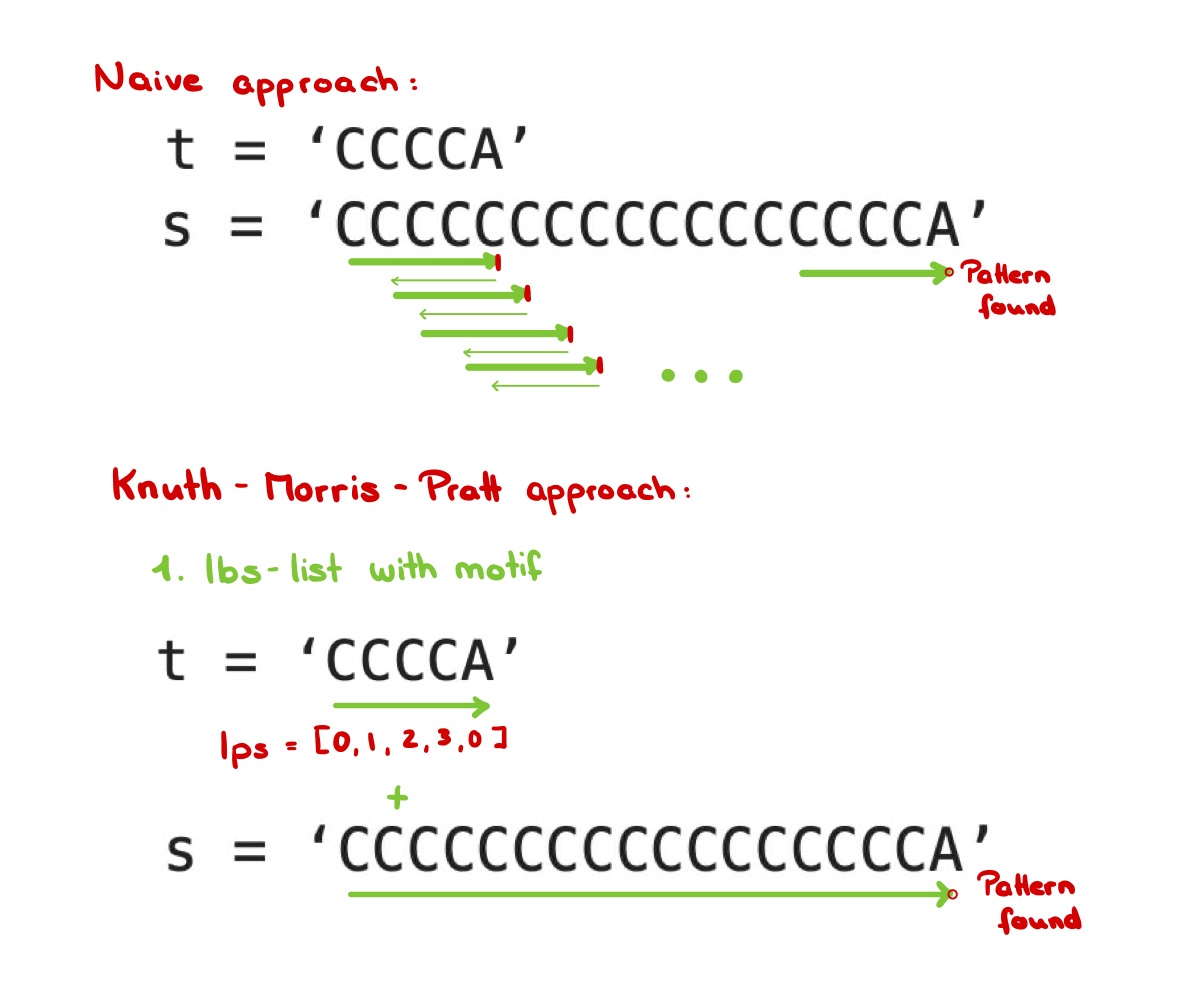
1. Naive Approach

Time complexity: O (nm)

Here, n represents the length of the complete DNA string and m for the length of the Motif.

Following my function that can be called with naive_search(s,t):

def naive_search(DNA, motif):
loc = set() #set for all starting-locations of motifs>
dnaShort = len(DNA) - len(motif) + 1>
for pos in range(dnaShort):
            counter = 0 #counting matches between DNA sequence and Motif
            for nucl in range(len(motif)):
            if motif[nucl] == DNA[pos + nucl]:
            counter += 1
            else:
            break
            if counter == len(motif):
            pos += 1
            loc.add(pos)
            #print(motif, "found at position", pos)

loc = sorted(loc)
print('Output:', *loc)

Even though the main focus of this post are different ways solving this problem, still following an explanation of a couple of lines:

Line 3 is built to change the value of in the range value in to prevent an “IndexError” in line 6.

Illustration for Line 3. — Originally I have used range(len(DNA)) instead of the calculated value of line 3.

However, this can cause errors in line 7 when coming to the end of the DNA sequence s:

How to solve this? One approach is just to insert an exception (try-except). Or instead, end the for-loop in line 4 earlier. I created dnaShort-value in line 3 for this purpose:

On another note: Generally Rosalind does not seem to like the answers in lists (or sets), so in line 17, you can find a great way to easily separate each value of the list with a space. Just add a star before the variable. Quite straight forward.

Check out the latest code on GitHub: Commit to Naive Approach

Author

Affiliation

Franziska Ahrend

Published

Jul. 14, 2022

DOI

2. KMP: Knuth-Morris-Pratt

With the Knuth-Morris-Pratt algorithm for pattern search, we want to eliminate the backtracking and instead create a list (the so-called lps-table) as a memorization of the pattern. This pattern is in the case of bioinformatics and in this specific problem the motif.

The time complexity of the previous introduced naive approach is O(nm). That approach does not work optimal when multiple matching nucleotides are followed eventually by a mismatch. Imagine we have a DNA sequence (s) with a motif (t) as followed:

s = ‘CCCCCCCCCCCCCCCCCA’
t = ‘CCCCA’

This displays the worst case of O(m(n-m+1)). The naive approach checks the pattern starting at each nucleotide (until length of DNA sequence is reached); it matches with the next four nucleotides, but then after the mismatch (Adenine vs Cytosine) it backtracks.

KMP solves this problem of those reoccurring pattern by using degenerating property. This takes advantage of the information that we already know from previous compared positions.

In our earlier example, after the mismatch at position 4 (starting at 0), the algorithm simply checks position 4 in the string for an Adenine. Anther mismatch, it checks position 5. And so on.

Naive vs KMP approach — Comparison of workflows between naive approach and KMP-algorithm

So KMP maximal needs to run once through the DNA sequence once plus throught the motif sequence:

Time complexity: O(n+m) = O(n)

Again, n represents the length of the complete DNA string and m for the length of the Motif.

I have mentioned the lps-list which gives information about the reoccurrence of the pattern. It therefore has the length of the motif (t). lps stands for “longest proper prefix which is likewise suffix” [1]. Following illustration should show how such table is constructed:

Due to this separation of two steps, I have also created two functions, which are showed in the following:

A) Building the lps-list:

def lpsTableBuild(motif, m, lps):
length = 0 #start of previous longest prefix suffix-length
lps[0] = 0 #impossible to have motif before motif start 
i = 1 #index of lps-list

#builds lps-table from positon i = 1 to m-1
while i < m:
            if motif[i]!= motif[length]:
            if length != 0:
            length = lps[length-1]
            else:
            lps[i] = 0
            i += 1
            else:   
            length += 1
            lps[i] = length
            i += 1
            
      print('\nlps-list:', lps)

def kmp_search(DNA, motif): 
    loc = set() #set for all starting-locations of motifs
    m = len(motif)
    n = len(DNA)
  
    lps = [0]*m #initialization of lps-table (list)
    lpsTableBuild(motif, m, lps)# Creating pattern-list
  
    i,j = 0,0 # index for DNA[] and motif[] 
    while i < n:
    if motif[j] == DNA[i]:
    i += 1
    j += 1
    if j == m: #match found
    #print(motif, "found at position", (i-j + 1))
    loc.add(i-j + 1) #add to set
    j = lps[j-1]
  
    #handling mismatches after matches (j) 
    elif i < n and motif[j] != DNA[i]:
    #we know match due to previous matches of pattern
    if j != 0:
    j = lps[j-1]
    else:
    i += 1
    loc = sorted(loc) 
    print('\nOutput:', *loc)

Check out the latest code on GitHub: Latest Commit

Next up:

3. Rabin-Carp

Coming soon...

4. Bozer-Moore

Coming soon...

Footnotes

[1] Garima Pandey,Nitin Arora, Mamta Martolia. “A Novel String Matching Algorithm and Comparison with KMP Algorithm” in International Journal of Computer Applications (0975 – 8887) Volume 179 – No.3, December 2017.